Pengertian Teorema pythagoras adalah suatu aturan matematika yang dapat digunakan untuk menentukan panjang salah satu sisi dari sebuah segitiga siku-siku, berikut ini kan disajikan contoh soal dan pembahasan Teorema Pythagoras. Mudah-mudahan contoh soal dan pembahasan Teorema Pythagoras ini bermanfaat banyak.
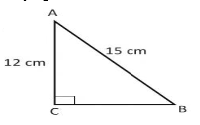
Soal No. 1) Perhatikan gambar!
Panjang BC adalah …..
a. 3 cm
b. 6 cm
c. 8 cm
d. 9 cm
Jawaban: D
Pembahasan:
BC = √(AB2 – AC2)
= √(152 – 122)
= √(225 – 144) = √81 = 9 cm
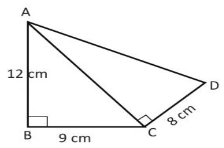
Soal No. 2) Perhatikan gambar! Panjang AD adalah …..
a. 15 cm
b. 17 cm
c. 24 cm
d. 25 cm
Jawaban: B
Pembahasan:
Perhatikan segitiga siku-siku ABC.
AC = √(AB2 + BC2)
= √(122 + 92)
= √(144 + 81) = √225
= 15 cm
Perhatikan segitiga siku-siku ACD.
AD = √(AC2 + CD2)
= √(152 + 82)
= √(225 + 64) = √289
= 17 cm
Soal No. 3) Perhatikan gambar!
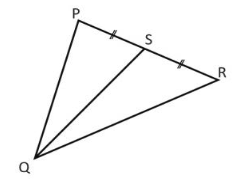
Garis QS adalah garis …..
a. Berat
b. Tinggi
c. Sumbu
d. Bagi
Jawaban: A
Pembahasan:
Perhatikan garis QS membagi sisi PR sama besar (PS = SR) maka garis QS adalah garis berat.
- (i) 3 cm, 4 cm, 5 cm
- (ii) 7 cm, 8 cm, 9 cm
- (iii) 5 cm, 12 cm, 15 cm
- (iv) 7 cm, 24 cm, 25 cm
Yang merupakan ukuran sisi segitiga siku-siku adalah …..
A. (i) dan (ii)
B. (i) dan (iii)
C. (ii) dan (iii)
D. (i) dan (iv)
Jawaban: D
Pembahasan:
Di antara empat buah segitiga yang merupakan tripel Pythagoras (segitiga siku-siku) adalah:
(i) 3 cm, 4 cm, 5 cm; dan
(iv) 7 cm, 24 cm, 25 cm
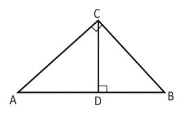
Soal No. 5) Pada gambar di bawah, di ketahui panjang AB = 9 cm dan AD = 5 cm. Panjang BC adalah …..
a. 4 cm
b. 5 cm
c. 6 cm
d. 8 cm
Jawaban: C
Pembahasan:
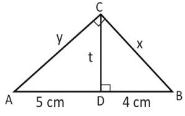
Perhatikan segitiga BCD
t2 = x2 – 42
= x2 – 16 …..(1)
Perhatikan segitiga ACD
t2 = y2 – 52
= x2 – 25 …..(2)
Substitusikan persamaan (1) dan (2).
x2 – 16 = y2 – 25
y2 = x2 – 16 + 25
y2 = x2 + 9 …..(3)
Perhatikan segitiga ABC berlaku:
x2 = 92 – y2
Substitusikan persamaan (3) maka:
x2 = 92 – (x2 + 9)
x2 + x2 = 81 – 9
2x2 = 72
x2 = 36
x = 6
Jadi, panjang BC adalah 6 cm.