Hai kawan-kawan, berikut ini akan disajikan Soal Essay Fisika (Vektor) Beserta Jawabannya. Mudah-mudahan Soal Essay Fisika (Vektor) Beserta Jawabannya ini memberikan manfaat yang banyak.
Soal No. 1). Diberikan 3 buah vektor F1=10 N, F2 =25 N dan F3=15 N seperti gambar berikut.
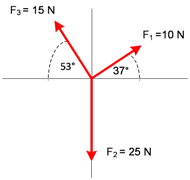
a. Resultan ketiga vektor
Jawaban
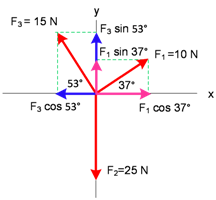
Vektor yang dalam perhitungan selanjutnya tidak digunakan lagi karena sudah diuraikan tadi, dihapus saja, agar kelihatan lebih bersih, sisanya seperti ini:
Jumlah komponen vektor-vektor pada sumbu x dan y :
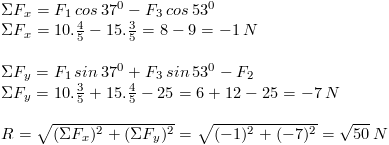
b. Mencari sudut yang terbentuk antara resultan vektor R dengan sumbu x
tan θ = ΣFy /ΣFx
tan θ = −7/−1 = 7
θ = arc. tan 7 = 81,87°
“Untuk dua buah vektor dengan besar yang sama dan membentuk sudut 120o maka resultan kedua vektor besarnya akan sama dengan besar salah satu vektor”
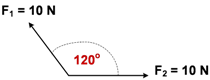
Pada soal di atas, 2 buah vektor (gaya) masing-masing 3 N membentuk sudut 120o, sehingga resultan kedua gaya juga 3 N. Resultan kedua gaya ini akan segaris dengan gaya 6 N, namun berlawanan arah. Sehingga dengan mudah soal ini bisa dijawab resultan ketiga gaya adalah 6 N dikurangi 3 N hasilnya adalah 3 N.
Soal No. 3). Diberikan dua buah vektor masing-masing vektor dan besarnya adalah A = 8 satuan, B = 10 satuan. Kedua vektor ini membentuk sudut 37°. Tentukan hasil dari:
b) A × BPembahasan!
a) A⋅ B adalah perkalian titik (dot) antara vektor A dan vektor B
Untuk perkalian titik berlaku
A⋅ B = A B cos θ
Sehingga
A⋅ B = A B cos 37° = (8)(10)(0,8) = 64 satuanb) A × B adalah perkalian silang (cross) vektor A dan vektor B
Untuk perkalian silang berlaku
A × B = A B sin θ
Sehingga
A × B = A B sin 37° = (8)(10)(0,6) = 48 satuan
B. 6
C. 7
D. 8
E. 12
Soal ini adalah soal penerapan perkalian titik (dot product ) antara vektor gaya F dan vektor perpindahan r dengan kedua vektor dalam bentuk i dan j atau vektor satuan. Besaran yang dihasilkan nantinya adalah skalar (usaha termasuk besaran skalar, hanya memiliki besar, tanpa arah). Usaha dilambangkan dengan W dari kata work.
W = F ⋅ r
26 = (2i + 3j)⋅ (4i + aj)
Cara perkalian titik dua vektor dalam bentuk i,j adalah yang i kalikan i, yang j kalikan j, hingga seperti berikut
26 = 8 + 3a
3a = 26 − 8
a = 18/3 = 6
i dan j nya jadi hilang karena i kali i atau j kali j hasilnya adalah satu.
Soal No. 5). Diketahui vektor a seperti pada gambar berikut.
Gambarkan vektor-vektor berikut.
a. 2a
b. –a
c. -1,5a
Jawaban
a. Vektor a mempunyai panjang 4 meter.
Vektor 2a mempunyai panjang anak panah sama dengan 2 × panjang anak panah a sehingga panjang vektor 2a adalah 8 meter dan arahnya searah dengan vektor a.
b. Vektor –a mempunyai panjang anak panah yang sama dengan vektor a tetapi arahnya berlawanan.
c. Vektor -1,5a mempunyai panjang anak panah sama dengan 1,5 × panjang anak panah a, yaitu 6 meter dan arahnya berlawanan dengan a.
Soal No. 6). Uraikan vektor berikut ini atas komponen-komponen terhadap sumbu X dan sumbu Y.
a. F1 = 60 satuan membentuk sudut 45o terhadap sumbu X.
b. F2 = 30 satuan membentuk sudut 135o terhadap sumbu X.
c. F3 = 80 satuan membentuk sudut 270o terhadap sumbu X.
Jawaban
Untuk menjawab pertanyaan tersebut, kita gambarkan dulu vektor-vektor tersebut ke dalam bidang XY sebagai berikut.
Soal No. 7). Vektor p mempunyai besar 5 satuan dan vektor q besarnya 3 satuan. Kedua vektor tersebut saling membentuk sudut 60o. Tentukan besar resultan kedua vektor tersebut.
Jawaban
Diketahui:
p = 5 satuan
q = 3 satuan
α = 60o
Besar resultan (R) dari kedua vektor tersebut dapat ditentukan dengan menggunakan persamaan
Soal No. 8). Tiga buah vektor digambarkan seperti gambar di bawah (1 skala = 1 satuan). Tentukan besar dan arah resultan ketiga vektor tersebut dengan menggunakan metode analitik.
Jawaban
Dari gambar, kita tentukan terlebih dahulu komponen-komponen tiap vektor.
A1x = + 5 satuan;
A1y = 0
A2x = 0;
A2y = 3 satuan
A3x = -5 satuan;
A3y = 3 satuan
Kemudian kita tentukan resultan vektor-vektor tersebut pada sumbu X dan sumbu Y.
Untuk sumbu X ; Untuk sumbu Y
∑Ax= A1x + A2x + A3x, ; ∑Ay = A1y + A2y + A3y
∑Ax= +5 + 0 + (-5) ,; ∑Ay= 0 + 3 + 3
∑Ax= 0 satuan ,; ∑Ay= 6 satuan
Karena ∑Ax= 0 dan ∑Ay searah sumbu Y sehingga arah resultan vektornya membentuk sudut 90 derajat terhadap sumbu X.
Besar ketiga vektor tersebut adalah
Jadi, besar resultan ketiga vektor tersebut adalah 6 satuan.
Soal No. 9). Lima buah vektor digambarkan sebagai berikut.
Besar dan arah vektor pada gambar tersebut adalah sebagai berikut.
Tentukan besar dan arah vektor resultan.
Jawaban
Untuk memudahkan dalam menentukan besar dan arah vektor resultan, dibuat tabel sebagai berikut.
Arah vektor R terhadap sumbu X positif
Soal No. 10). Diketahui koordinat titik A adalah (2, -4, 5). Tuliskan dalam bentuk vektor dan berapa besarnya?
Jawaban
Vektor A = 2i + (-4)j + 5k
= 2i – 4j + 5k
